§4.2 换元积分法
一、第一类换元法
设![]() 具有原函数
具有原函数![]() ,即
,即
![]() ,
,
![]() 。
。
若![]() 又是另一新变量
又是另一新变量![]() 的函数
的函数![]() , 且
, 且![]() 可微,由复合函数的微分法有
可微,由复合函数的微分法有 ![]() ,从而
,从而
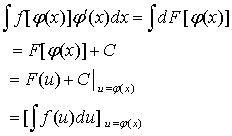
综合上述讨论,有
【定理一】设![]() 具有原函数,
具有原函数,![]() 可导,则有换元积分公式
可导,则有换元积分公式
![]()
这个定理表明:欲求不定积分![]() ,可令
,可令![]() ,则不定积分化为
,则不定积分化为![]() ,它将原来的积分变量
,它将原来的积分变量![]() 换成了新的积分变量
换成了新的积分变量![]() ,求出不定积分
,求出不定积分![]() 之后,再把
之后,再把![]() 代换回去。
代换回去。
【例1】求下列不定积分
1、![]() , 2、
, 2、![]() , 3、
, 3、![]()
解1
令
![]() ,
, ![]() ,
,
![]() 。
。
解2
令
![]() ,
, ![]() ,
,
![]() 。
。
解3
令
![]() ,
, ![]() ,
,
![]() 。
。
由上面的解题可发现,变量![]() 只是一个中间变量,在求不定积分的过程中,只是起过渡作用,最终都要换回到原来的积分变量。因此,在较熟练之后,可以采用不直接写出中间变量的做法。
只是一个中间变量,在求不定积分的过程中,只是起过渡作用,最终都要换回到原来的积分变量。因此,在较熟练之后,可以采用不直接写出中间变量的做法。
例如:
![]()
![]()
![]()
研究这些解法可观察到一个非常鲜明的特点:
将被积表达式凑成某个函数的微分形式,再利用积分运算与微分运算的互逆性,达到求不定积分的目的。
因此,第一类换元法又俗称为“凑微分法”。
【典型例题】
求不定积分 ![]() 。
。
解:
由复合函数求微分的脱衣原理, 有
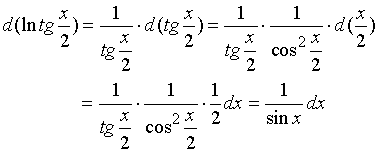
于是我们有下述典型的凑微分过程:
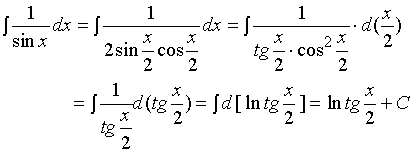
显而易见,凑微分过程与用脱衣原理求复合函数微分过程是完全相反的。因此,凑微分的过程可视为运用“穿衣原理”进行穿衣的过程 --- 即:后脱的衣服应先穿(或:先脱的后穿)。
一般来说,小孩子是先学会脱衣服,再学会穿衣服。这是由于穿衣服有个次序问题。因此,用凑微分法求不定积分较用脱衣原理求复合函数的导数要困难得多。
【例2】求

解:
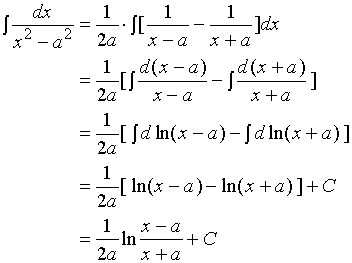
【例3】求 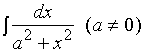
解:

二、第二类换元法
第一类换元法:
![]()
有时会遇到相反情形:![]()
显然,这类换元公式成立需要一定的条件,我们来探讨一下它所需要条件。
(1)、![]() 代换应可导;
代换应可导;
(2)、等式右端的不定积分要存在,即![]() 存在着原函数;
存在着原函数;
(3)、求出![]() 后,必须用
后,必须用![]() 的反函数
的反函数![]() 代回去,这样,需要函数
代回去,这样,需要函数![]() 具有反函数。
具有反函数。
【定理二】若
1、![]() 是单调函数;
是单调函数;
2、![]() 可导, 且
可导, 且![]() ;
;
3、![]() 具有原函数
具有原函数![]()
则有换元公式
![]()
其中:![]() 是
是 ![]() 的反函数。
的反函数。
【证明】
令 ![]() , 则
, 则
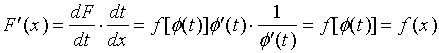 ,
,
这表明:![]() 是
是![]() 的原函数, 于是有:
的原函数, 于是有:
![]()
【例4】求![]()
解:令 ![]()
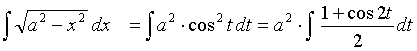
![]()
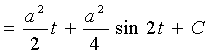
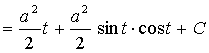
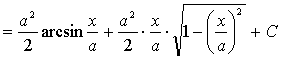
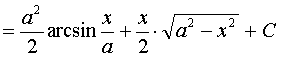
【例5】求 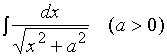
解:
令 ![]()
![]() ,
, 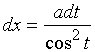 ,
,
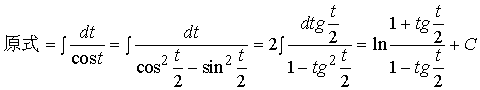
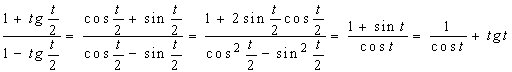
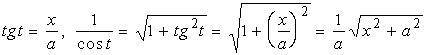
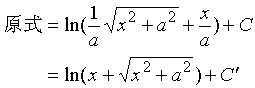
这里:
![]()
对此例,我们给出两点注解:
1、对于第二类换元法,求反函数是一个麻烦的地方,往往需要一定的技巧。上例的反函数不能简单地用![]() ,并将它代入
,并将它代入 中,得到
中,得到 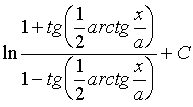 这个“形式过重”表达式,因为它不便应用。
这个“形式过重”表达式,因为它不便应用。
2、这一不定积分是一个重要的积分公式。
第二类换元法有一个十分有用的代换
—— 倒置代换![]() 。这一代换处理某些不定积分功效显著 (用它可消去被积函数的分母中的因子,
特别是幂次为偶数的情形)。
。这一代换处理某些不定积分功效显著 (用它可消去被积函数的分母中的因子,
特别是幂次为偶数的情形)。
【例6】求 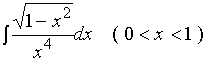
解:
令 ![]()

最后,我们指出:使用变量替换求不定积分,关键是选择恰当的替换,这需要经验。记往! 不适宜的替换会使问题弄得愈来愈复杂。